
FACSanadu is a program for flow cytometry, supporting FCS files and COPAS Biosorter files. It is designed to allow you to visualize and quantify your flow cytometry data with a minimum of effort.
Known bugs: Not all FCS files are supported. It depends on your machine. We are happy to get files sent to us if they don’t work as we can then use these for testing our code.
Mac users are likely to have problems! Check out this link on running unsigned software to overcome this problem (if someone with a mac could help us sign the software, it would be great).
Download
Binary releases:
Example data to play with (unzip before opening):
If you are interested in the source code, proceed to GitHub. There is also statistics on OpenHub.
A bit on the design
FACSanadu is not designed to function as other FACS software, and this is to be regarded as conscious choice. In particular, we wanted to avoid having the classical layout where panels can be added at random locations. Also, gating is only ever truly meaningful if it is done the same way on all the samples, and thus this is enforced in the design (it might one day be relaxed). As such, gates are shared between datasets, and moving it in one dataset will directly move it in another. You will normally work with a list of FCS-files, seldom just one.
To get acquainted, first load a few datasets in the top-left corner “Add dataset”. You can select multiple in one go. Or even more convenient, drag-and-drop FCS-files into this list. If you have COPAS files, drag the DAT-files.
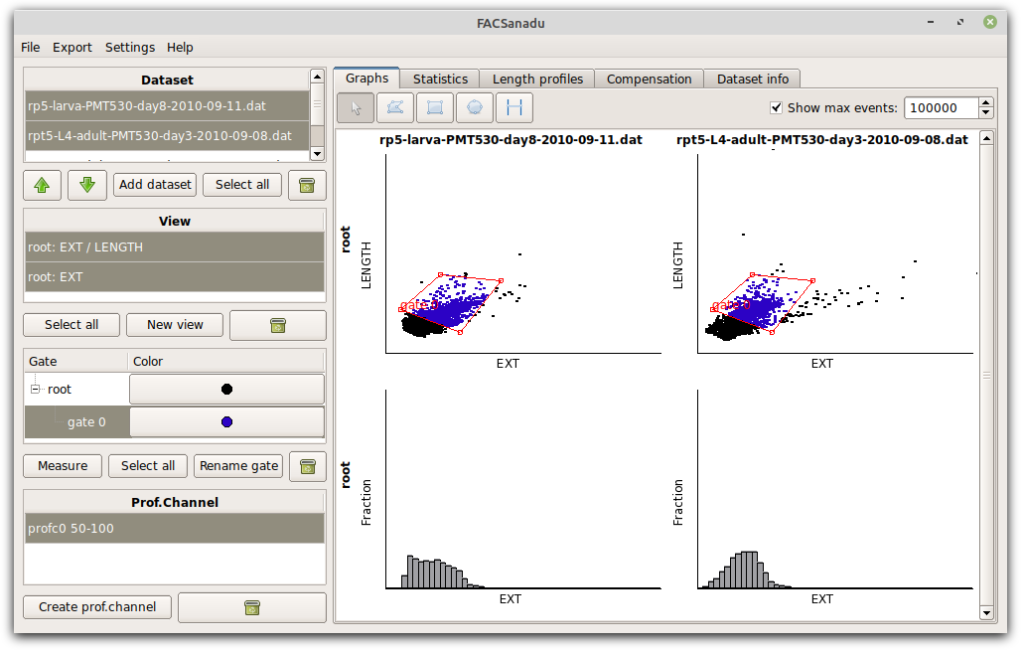
Another design choice is that we usually want to compare different datasets, and so the software is optimized for showing multiple datasets next to each other. This led to the current grid layout as shown below. Datasets are shown horizontally, and different views of it vertically (additional views can be added with “New view” to the left). Views are either scatter plots or histograms. Scatter plots can be log-transformed. All of these settings are made by left-clicking on any axis.
FACSanadu supports a minimum of gates – polygons, rectangles, ellipsoids and histogram ranges. Gates that you draw will copy the settings of the channel, which especially includes log transformation (on/off) and which subset of the population you are looking at.
Once gates have been set, you can extract population statistics. This is in a separate tab (Figure below). You can choose to see either % cells of everything, or % cells of the parent gate (gates are organized hierarchically as in most other software).
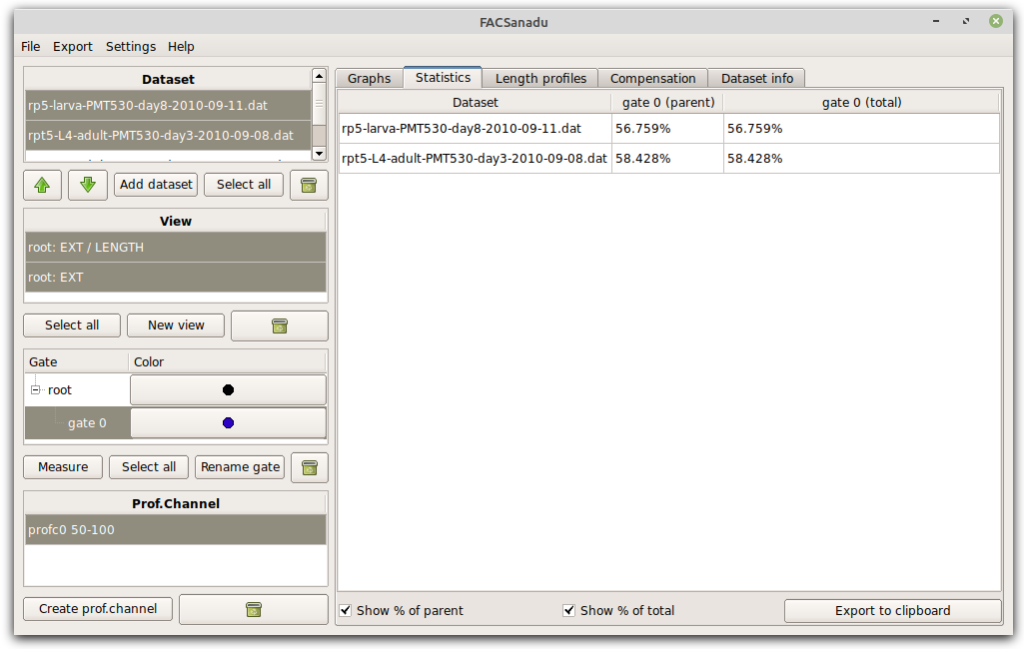
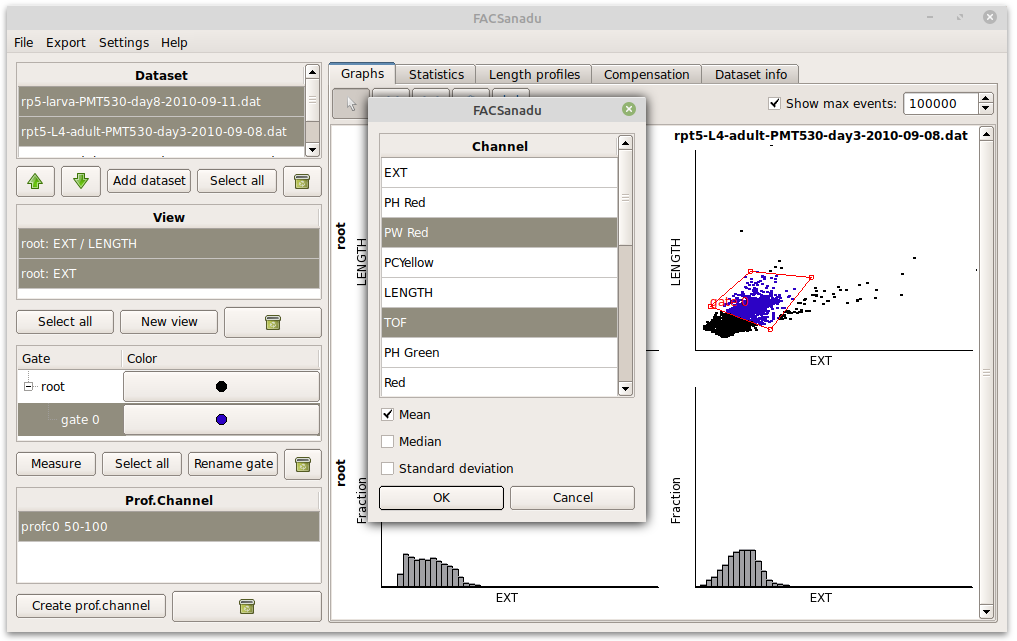
As an additional feature you can also add Measures (Figure below – select a gate and press “Add measure”). These allow you to, within a population, measure the Mean, Median and Variance of the fluorescence of points. These can be an alternative to the binary way of counting cells. New measures will appear in the statistics view.
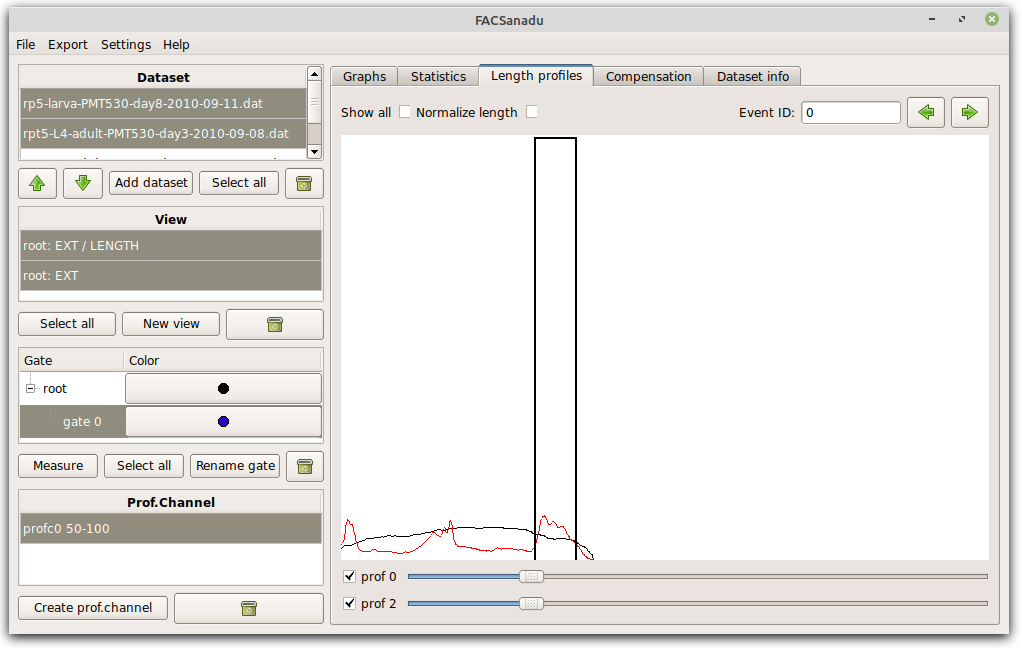
Those still having a COPAS biosorter can look at their data in the tab “Length profiles” (Figure below). Upon loading COPAS data, all length profiles are automatically flipped as needed for normalization. You can then choose to “Normalize length” depending on the need for your project. From these profiles you can calculate the average along one part of the profile by choosing “Add prof.chan”. Before doing so, only have the channel visible that you want to measure, and normalize length if needed. This is now stored as a “profile channel”, and can be treated as any normal channels, for viewing and gating.
You can export the data if you want to look at it in e.g. R or Python. Exporting will include any COPAS profile measurements as an additional column. See the “Export” menu above.
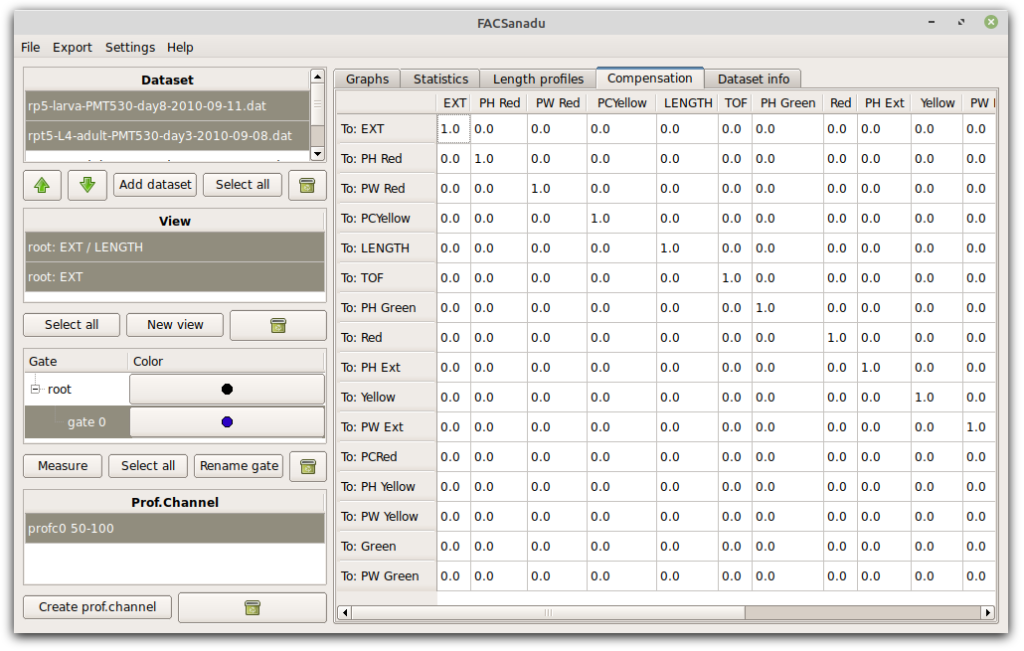
FACSanadu has basic functionality for compensation. You can edit the matrix directly in a separate tab; however, there is not yet any way to automatically calculate the values.
Contact
We are looking for a software engineering student who can, as a master thesis project or similar, help us get this software ironed out for final publication. Let us know if interested. Ideally you know Java, C# or C++, but any object oriented experience helps! Or if not object oriented, at least a good amount of experience in a less structured language. The task may end up including a total rewrite based on our previous experience, and possibly moving to JavaFX instead of QT for the interface. Optionally, it may make sense to produce an online system to be deployed in the cloud.
This software is now released as a stable version but we still expect more testing to be needed, in particular with data from other instruments than ours. Please send any bug reports or feature requests to johan.henriksson AT umu . org. You will then of course be informed once it has been resolved!
*So is this old game
